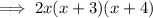Answer:
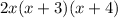
Explanation:
To factor
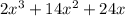
First, factor out the common term
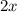 :
:
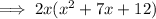
Now factor the expression in the parantheses:
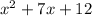
Find two numbers that multiply to 12 and sum to 7: 3 and 4
Rewrite
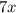 as the sum of these 2 numbers:
as the sum of these 2 numbers:
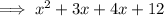
Factorize the first two terms and the last two terms separately:
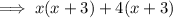
Factor out the common term
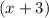 :
:
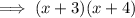
Therefore, the final factorization of the polynomial is: