Answer:
The minimum sample size required is 71.
Explanation:
The (1 - α)% confidence interval for population mean is:
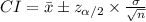
The margin of error for this interval is:
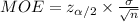
It is provided that the population standard deviation σ can be estimated by the sample standard deviation s.
The given information is:
s = 18000,
Margin of error = $4200.
Confidence level = 95%
The z-value for 95% confidence level is,
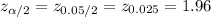
*Use a z-table for the critical value.
Compute the sample size required as follows:
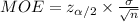
![n=[(z_(\alpha/2)* \sigma )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/gbu8dccknpsvacjukdw18e3gr03mgnrwz1.png)
![=[(18000* 1.96)/(4200)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/7vu65ys73zdisbyjw4h19p3zhvw1ay4a1y.png)
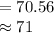
Thus, the minimum sample size required is 71.