Question

An ice skater with a mass of 52.5 kg is gliding across a smooth lake with a speed of 2.25 m/s when she hits a spot of ice covered with snow. After a time of 7.55 s she has slowed to a stop. Using your knowledge of momentum, determine the magnitude of the average force of friction acting on the ice skater while she slows to a stop.

Answer 1

The magnitude of the average force of friction acting on the ice skater while she slows to a stop is 15.65 N

Step-by-step explanation:

Given;

mass of the ice skater, m = 52.5 kg

speed of the ice skater, u = 2.25 m/s

time for her gliding, t = 7.55 s

To determine the magnitude of the average force of friction acting on the ice skater while she slows to a stop, we apply Newton's second law of motion;

F = ma

`But, a = (v-u)/(t)`

`F =m ((v-u)/(t))`

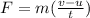
where;

F is average force of friction acting on the ice skater

v is the final speed speed of the ice skater = 0

u is the initial speed of the ice skater

t is time

`F = m((v-u)/(t) )\\\\F = 52.5((0-2.25)/(7.55))\\\\F = -15.65 \ N`

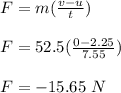
Thus, the magnitude of the average force of friction acting on the ice skater while she slows to a stop is 15.65 N