Answer:
790.904 kg/s
Step-by-step explanation:
From the ideal gas properties table
At T₁ =310K
h₁ =310.240 kJ/kg
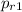 = 1.5546
= 1.5546
s₁⁰ =1.73498 kJ/kg K
Process 1-2s is isentropic compression (shown in the attached diagram)
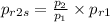
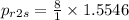
= 8 × 1.5546
= 12.43
now enthalpy
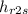 = 562.46 kJ/kg
= 562.46 kJ/kg
Actual enthalpy at state 2 is given by
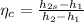
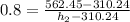
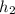 = 625.50 kJ/kg
= 625.50 kJ/kg
Process 3 - 4s is isentropic expansion
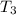 = 900K
= 900K
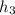 = 932.93kJ/kg
= 932.93kJ/kg
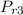 = 75.29
= 75.29
hence
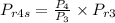
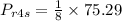
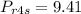
Enthalpy at state 4
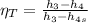
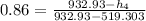
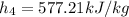
the net work output
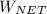 is given by
is given by


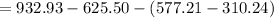
= 40.46kJ/kg
Power output = mass flow rate × net work output
32 × 10³ = m × 40.46
m = 790.904 kg/s