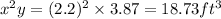Question

A rectangular box with a square base is to be constructed from material that costs $9 per ft2 for the bottom, $5 per ft2 for the top, and $4 per ft2 for the sides. Find the box of greatest volume that can be constructed for $204. Round your answer to 2 decimals. slader -g

Answer 1

`18.73ft^3`

Explanation:

Let

Side of square base=x

Height of rectangular box=y

Area of square base=Area of top=
`(side)^2=x^2`

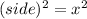
Area of one side face=
`l* b=xy`

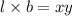
Cost of bottom=$9 per square ft

Cost of top=$5 square ft

Cost of sides=$4 per square ft

Total cost=$204

Volume of rectangular box=
`V=lbh=x^2y`

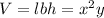
Total cost=
`9(x^2)+5x^2+4(4xy)=14x^2+16xy`

`204=14x^2+16xy`

`204-14x^2=16xy`

`y=(204-14x^2)/(16x)=(102-7x^2)/(8x)`

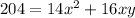
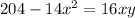
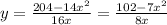
Substitute the values of y

`V(x)=x^2* (102-7x^2)/(8x)=(1)/(8)(102x-7x^3)`

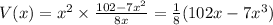
Differentiate w.r.t x

`V'(x)=(1)/(8)(102-21x^2)=0`

`V'(x)=0`

`(1)/(8)(102-21x^2)=0`

`102-21x^2=0`

`102=21x^2`

`x^2=(102)/(21)=4.85`

`x=√(4.85)=2.2`

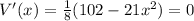
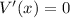
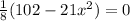
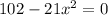
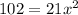
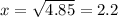
It takes positive because side length cannot be negative.

Again differentiate w.r. t x

`V''(x)=(1)/(8)(-42x)`

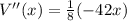
Substitute the value

`V''(2.2)=-(42)/(8)(2.2)=-11.55<0`

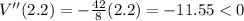
Hence, the volume of box is maximum at x=2.2 ft

Substitute the value of x

`y=(102-7(2.2)^2)/(8(2.2))=3.87 ft`

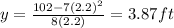
Greatest volume of box=
`x^2y=(2.2)^2* 3.87=18.73 ft^3`