Answer:
Explanation:
REcall that all the points of the unit circle have the following coordinates
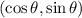 , where theta is the angle in standard position (that is, with the terminal side on the given point and the initial side on the x-axis).
, where theta is the angle in standard position (that is, with the terminal side on the given point and the initial side on the x-axis).
Then in this case we have that
![\cos\theta = \frac{1}{\sqrt[]{10}}, \sin \theta =\frac{-3}{\sqrt[]{10}}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/2nqxhlfpznhq4yrfo1afw32jj61ldgelnw.png) .
.
Recall that
![\tan \theta = (\sin \theta)/(\cos \theta) = \frac{\frac{-3}{\sqrt[]{10}}}{\frac{1}{\sqrt[]{10}}} = -3](https://img.qammunity.org/2021/formulas/mathematics/middle-school/vbraajt6izmgds4fioq6s3tbmlwlb58mgt.png)