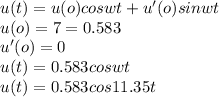Question

A mass weighting 16 lbs stretches a spring 3 inches. The mass is in a medium that exerts a viscous resistance of 20 lbs when the mass has a velocity of 4 ft/sec. Suppose the object is displaced an additional 7 inches and released. Find an equation for the object's displacement, u(t), in feet after t seconds.

Answer 1

The equation for the object's displacement is
`u(t)=0.583cos11.35t`

Step-by-step explanation:

Given:

m = 16 lb

δ = 3 in

The stiffness is:

`k=(m)/(\delta ) =(16)/(3) =5.33lb/in`

The angular speed is:

`w=\sqrt{(k)/(m) } =\sqrt{(5.33*386.4)/(16) } =11.35rad/s`

The damping force is:

`F_(D) =cu`

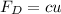
Where

FD = 20 lb

u = 4 ft/s = 48 in/s

Replacing:

`c=(F_(D) )/(u) =(20)/(48) =0.42lbs/in`

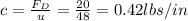
The critical damping is equal:

`c_(c) =(2k)/(w) =(2*5.33)/(11.35) =0.94lbs/in`

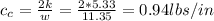
Like cc>c the system is undamped

The equilibrium expression is:

`u(t)=u(o)coswt+u'(o)sinwt\\u(o)=7=0.583\\u'(o)=0\\u(t)=0.583coswt\\u(t)=0.583cos11.35t`