Answer:
(a) The time the T-shirt takes to maximum height is 2 seconds
(b) The maximum height is 68 ft
(c) The range of the function that models the height of the T-shirt over time given above is

Explanation:
Here, we note that the general equation representing the height of the T-shirt as a function of time is

Where:
h = Height reached by T-shirt
t = Time of flight
u = Initial velocity = 64 ft/s
g = Acceleration due to gravity (negative because upward against gravity) = 32 ft/s²
h₁ = Initial height of T-shirt = 4 ft
(a) The maximum height can be found from the time to maximum height given as
v = u - gt
Where:
u = Initial velocity = 64 ft/s
v = Final upward velocity at maximum height = 0 m/s
g = 32 ft/s²
Therefore,
0 = 64 - 32·t
32·t = 64 and
t = 64/32 = 2 seconds
(b) Therefore, maximum height is then

∴ h = 68 ft
The T-shirt is then caught 41 ft above the court on its way down
(c) The range of the function that models the height of the T-shirt over time given above is derived as

With u = 64 ft/s
g = 32 ft/s² and
h₁ = 4 ft
The equation becomes
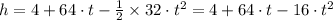 .
.