Question

During halftime of a basketball ​game, a sling shot launches​ T-shirts at the crowd. A​ T-shirt is launched from a height of 4 feet with an initial upward velocity of 64 feet per second. The​ T-shirt is caught 41 feet above the court. How long will it take the​ T-shirt to reach its maximum​ height? What is the maximum​ height? What is the range of the function that models the height of the​ T-shirt over​ time?

Answer 1

(a) The time the T-shirt takes to maximum height is 2 seconds

(b) The maximum height is 68 ft

(c) The range of the function that models the height of the T-shirt over time given above is
`4 + 64\cdot t - 16 \cdot t^(2)`

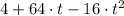
Explanation:

Here, we note that the general equation representing the height of the T-shirt as a function of time is

`h = h_1 + u\cdot t - (1)/(2) \cdot g \cdot t^(2)`

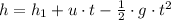
Where:

h = Height reached by T-shirt

t = Time of flight

u = Initial velocity = 64 ft/s

g = Acceleration due to gravity (negative because upward against gravity) = 32 ft/s²

h₁ = Initial height of T-shirt = 4 ft

(a) The maximum height can be found from the time to maximum height given as

v = u - gt

Where:

u = Initial velocity = 64 ft/s

v = Final upward velocity at maximum height = 0 m/s

g = 32 ft/s²

Therefore,

0 = 64 - 32·t

32·t = 64 and

t = 64/32 = 2 seconds

(b) Therefore, maximum height is then

`h = 4 + 64* 2 - (1)/(2) * 32 * 2^(2)`

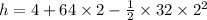
∴ h = 68 ft

The T-shirt is then caught 41 ft above the court on its way down

(c) The range of the function that models the height of the T-shirt over time given above is derived as

`h = h_1 + u\cdot t - (1)/(2) \cdot g \cdot t^(2)`

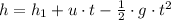
With u = 64 ft/s

g = 32 ft/s² and

h₁ = 4 ft

The equation becomes

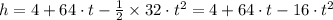`h =4 + 64\cdot t - (1)/(2) * 32 \cdot t^(2) = 4 + 64\cdot t - 16 \cdot t^(2)`.