Question

A 10 kg box is being pushed across a rough surface with constant speed of 2 m/s. The person pushing the box slips and stops pushing. The box continues to slide across the surface before coming to rest. If the coefficient of friction between the crate and the surface is 0.1, how far does the box travel before coming to rest?

A) 0.5 m
B) 1.0 m
C) 2.0 m
D) 4.0 m
E) 8.0 m

Answer 1

2.04 m

Step-by-step explanation:

Parameters given:

Mass of box, m = 10 kg

Initial speed of box, u = 2 m/s

Final velocity of box, v = 0 m/s (The box comes to rest)

Coefficient of friction, μ = 0.1

To find the distance moved by the box, we need to use one of Newton's equation of linear motion:

`v^2 = u^2 + 2as`

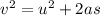
where a = acceleration and s = distance moved

We don't have acceleration, a, but we can get this by first finding the frictional force. This is because we know that the frictional force will have equal magnitude but opposite direction as the force exerted by the box on the floor.

Frictional force is given as:

Fr = μmg

where g = acceleration due to gravity

Fr = 0.1 * 10 * 9.8

Fr = 9.8 N

The force exerted by the box on the floor will be -9.8 N.

Force is given as:

F = ma

-9.8 = 10 * a

a = -9.8/10 = -0.98
`m/s^2`

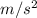
This shows that it is a deceleration because the box is slowing down.

Going back to the equation of motion:

`v^2 = u^2 + 2as`

`0^2 = 2^2 + (2*-0.98 *s)`

`0 = 4 - 1.96s\\\\\\1.96s = 4\\\\\\s = 4/1.96\\\\\\s = 2.04 m`

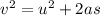
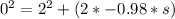
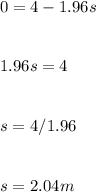
The distance moved by the box is 2.04 m