a. Given that y = f(x) and f(0) = -2, by the fundamental theorem of calculus we have
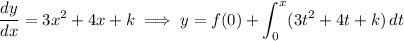
Evaluate the integral to solve for y :
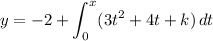
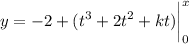
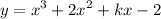
Use the other known value, f(2) = 18, to solve for k :
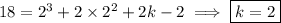
Then the curve C has equation
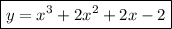
b. Any tangent to the curve C at a point (a, f(a)) has slope equal to the derivative of y at that point:
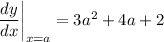
The slope of the given tangent line
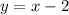 is 1. Solve for a :
is 1. Solve for a :
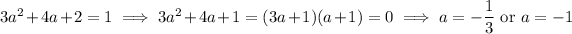
so we know there exists a tangent to C with slope 1. When x = -1/3, we have y = f(-1/3) = -67/27; when x = -1, we have y = f(-1) = -3. This means the tangent line must meet C at either (-1/3, -67/27) or (-1, -3).
Decide which of these points is correct:
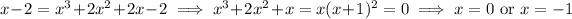
So, the point of contact between the tangent line and C is (-1, -3).