Given:
The given function is
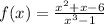
We need to determine the horizontal and vertical asymptote.
Horizontal asymptote:
From the given function, it is obvious that the denominator's degree is greater than the numerator's degree.
Then, the horizontal asymptote is the x - axis.
Thus, the horizontal asymptote is

Vertical asymptote:
The vertical asymptote of the rational function are the undefined points and can be determined by equating the denominator equal to zero.
Thus, we have;
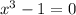

Solving, we get;
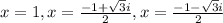
Thus, the function is undefined at the point

Hence, the vertical asymptote of the function is
