Question

A coffee distributor needs to mix a(n) Gazebo coffee blend that normally sells for $10.20 per pound with a Kona coffee blend that normally sells for $12.20 per pound to create 70 pounds of a coffee that can sell for $10.91 per pound. How many pounds of each kind of coffee should they mix

Answer 1

Let x represent pounds of Gazebo coffee and y represent pounds of Kona coffee.

We are told that a coffee distributor wants 70 pounds of coffee. We can represent this information in an equation as:

`x+y=70...(1)`

`y=70-x...(1)`

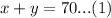
We have been given that Gazebo coffee blend sells for $10.20 per pound, so cost of x pounds of Gazebo coffee would be
`10.20x`.

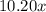Kona coffee blend sells for $12.20 per pound, so cost of y pounds of Kona coffee would be
`12.20y`.

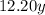Cost of 70 pounds of a coffee that can sell for $10.91 per pound would be
`70(10.91)`.

`10.20x+12.20y=70(10.91)...(2)`

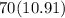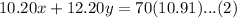
Upon substituting equation (1) in equation (2), we will get:

`10.20x+12.20(70-x)=70(10.91)`

`10.20x+854-12.20x=763.7`

`-2x+854=763.7`

`-2x+854-854=763.7-854`

`-2x=-90.3`

`(-2x)/(-2)=(-90.3)/(-2)`

`x=45.15`

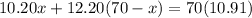
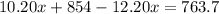
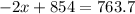
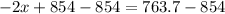
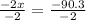
Therefore, distributor should use 45.15 pounds of Gazebo coffee.

Upon substituting
`x=45.15` in equation (1), we will get:

`y=70-14.15=24.85`

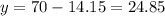
Therefore, distributor should use 24.85 pounds of Kona coffee.