Let x represent pounds of Gazebo coffee and y represent pounds of Kona coffee.
We are told that a coffee distributor wants 70 pounds of coffee. We can represent this information in an equation as:
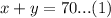
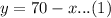
We have been given that Gazebo coffee blend sells for $10.20 per pound, so cost of x pounds of Gazebo coffee would be
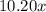 .
.
Kona coffee blend sells for $12.20 per pound, so cost of y pounds of Kona coffee would be
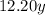 .
.
Cost of 70 pounds of a coffee that can sell for $10.91 per pound would be
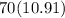 .
.
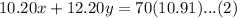
Upon substituting equation (1) in equation (2), we will get:
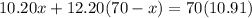
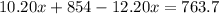
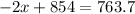
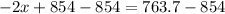
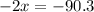
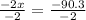
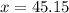
Therefore, distributor should use 45.15 pounds of Gazebo coffee.
Upon substituting
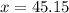 in equation (1), we will get:
in equation (1), we will get:
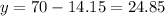
Therefore, distributor should use 24.85 pounds of Kona coffee.