Question

A 392 N wheel comes off a moving truck and rolls without slipping along a highway. At the bottom of a hill it is rotating at 25.0 rad/s. The radius of the wheel is 0.600 m, and its moment of inertia about its rotation axis is 0.800MR2. Friction does work on the wheel as it rolls up the hill to a stop, a height habove the bottom of the hill; this work has absolute value 2600 J. Calculate h.

Answer 1

The value of h is 14 meters

Step-by-step explanation:

Given that,

Weight of the wheel, F = 392 N

Angular velocity of the wheel,
`\omega=25\ rad/s`

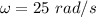
Radius of the wheel, r = 0.6 m

The moment of inertia about its rotation axis is,
`I=0.8\ mr^2`

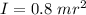
Work done by the wheel, W = 2600 J

Initially, the wheel has both translational and rotational kinetic energy such that,

`E_r+E_t-W=PE\\\\(1)/(2)I\omega^2+(1)/(2)mv^2-W=mgh`

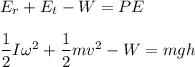
Use
`v=r\omega`

`(1)/(2)* 0.8mr^2\omega^2+(1)/(2)m\omega^2r^2-W=mgh\\\\(1)/(2)* 0.8* (392)/(9.8)* 0.6^2* (25)^2+(1)/(2)* (392)/(9.8)* (25)^2* (0.6)^2-2600=mgh\\\\h=(5500)/(mg)\\\\h=(5500)/(40\cdot9.8)\\\\h=14.03\ m`

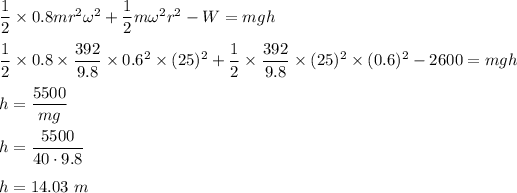
So, the value of h is 14 meters.