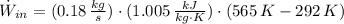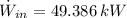Question

Air enters an adiabatic compressor at 104 kPa and 292 K and exits at a temperature of 565 K. Determine the power (kW) for the compressor if the inlet volumetric flow rate is 0.15 m3/s. Use constant specific heats evaluated at 300 K.

Answer 1

`\dot W_(in) = 49.386\,kW`

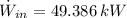
Step-by-step explanation:

An adiabatic compressor is modelled as follows by using the First Law of Thermodynamics:

`\dot W_(in) + \dot m \cdot c_(p)\cdot (T_(1)-T_(2)) = 0`

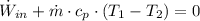
The power consumed by the compressor can be calculated by the following expression:

`\dot W_(in) = \dot m \cdot c_(v)\cdot (T_(2)-T_(1))`

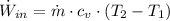
Let consider that air behaves ideally. The density of air at inlet is:

`P\cdot V = n\cdot R_(u)\cdot T`

`P\cdot V = (m)/(M)\cdot R_(u)\cdot T`

`\rho = (P\cdot M)/(R_(u)\cdot T)`

`\rho = ((104\,kPa)\cdot (28.02\,(kg)/(kmol)))/((8.315\,(kPa\cdot m^(3))/(kmol\cdot K) )\cdot (292\,K))`

`\rho = 1.2\,(kg)/(m^(3))`

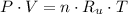
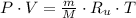
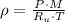
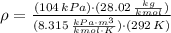
The mass flow through compressor is:

`\dot m = \rho \cdot \dot V`

`\dot m = (1.2\,(kg)/(m^(3)))\cdot (0.15\,(m^(3))/(s) )`

`\dot m = 0.18\,(kg)/(s)`

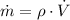
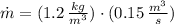
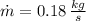
The work input is:

`\dot W_(in) = (0.18\,(kg)/(s) )\cdot (1.005\,(kJ)/(kg\cdot K))\cdot (565\,K-292\,K)`

`\dot W_(in) = 49.386\,kW`