Answer:
(a) 2.13*10^{-5} N
(b) 2.13*10^{-5} N
(c) 0 N
Step-by-step explanation:
the magnitude of the magnetic field generated by the wire is:
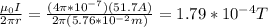
if we assume that the current is in the +y direction, B is in the +z direction.
(a) toward the wire, electron is in the -x direction. The angle between B and v is 90°. By using the following formula we obtain:
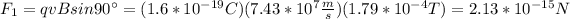
(b) parallel to the wire, electron is in the +y direction. Again angle between B ans v is 90°.

(c) perpendicular to both previous directions, that is, +z or -z. In this case velocity vector is parallel to the magnetic field vector. Hence:
F3=0N
hope this helps!