Answer:
a) p = 0.1808
b) Since 341.54 ≥ 10. Therefore the requirements for constructing a confidence interval for p is satisfied.
c) The interval is (0.1676, 0.194)
d) We are 90% confident that the population proportion of adult Americans who have donated blood in the past two years is between 0.1676 and 0.194
Explanation:
Given that:
n = 2306 and x =417
a) Obtain a point estimate for the population proportion (p) is the ratio of sample successes to sample size.
Therefore: p = x / n = 417 / 2306 = 0.1808
p = 0.1808
b) requirements for constructing a confidence interval for p is given by:
np(1-p) ≥ 10
Therefore: np(1-p) = 2306(0.1808)(1 - 0.1808) = 341.54 ≥ 10
Since 341.54 ≥ 10. Therefore the requirements for constructing a confidence interval for p is satisfied.
c) c = 90% = 0.9
α = 1 - 0.9 = 0.1
α / 2 = 0.1 /2 = 0.05
From the probability table,
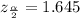
Margin of error (e) =

The boundaries are (p - e, p + e) = (0.1808 - 0.0132, 0.1808 + 0.0132) = (0.1676, 0.194)
The interval is (0.1676, 0.194)
d) We are 90% confident that the population proportion of adult Americans who have donated blood in the past two years is between 0.1676 and 0.194