Question

A survey of 2306 adult Americans aged 18 and older conducted by Harris Interactive found that 417 have donated blood in the past two years.

(a) Obtain a point estimate for the population proportion of adult Americans aged 18 and older who have donated blood in the past two years.
(b) Verify that the requirements for constructing a confidence interval about p are satisfied.
(c) Construct a 90% confidence interval for the population proportion of adult Americans who have donated blood in the past two years.
(d) Interpret the interval.

Answer 1

Answer is:

A. 0.1808

B.np(1-p)>=10, and sample is less than 5% of the population.

C. (0.1676, 0.1940)

D. We are 90% confidence interval for the population proportion of adult Americans who have donated blood in the past two years is between 0.1676 and 0.1940.

Refer below.

Explanation:

Refer to the pictures for brief explanation.

Answer 2

a) p = 0.1808

b) Since 341.54 ≥ 10. Therefore the requirements for constructing a confidence interval for p is satisfied.

c) The interval is (0.1676, 0.194)

d) We are 90% confident that the population proportion of adult Americans who have donated blood in the past two years is between 0.1676 and 0.194

Explanation:

Given that:

n = 2306 and x =417

a) Obtain a point estimate for the population proportion (p) is the ratio of sample successes to sample size.

Therefore: p = x / n = 417 / 2306 = 0.1808

p = 0.1808

b) requirements for constructing a confidence interval for p is given by:

np(1-p) ≥ 10

Therefore: np(1-p) = 2306(0.1808)(1 - 0.1808) = 341.54 ≥ 10

Since 341.54 ≥ 10. Therefore the requirements for constructing a confidence interval for p is satisfied.

c) c = 90% = 0.9

α = 1 - 0.9 = 0.1

α / 2 = 0.1 /2 = 0.05

From the probability table,
`z_{(\alpha)/(2) } = 1.645`

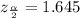
Margin of error (e) =
`z_{(\alpha)/(2) } \sqrt{(p(1-p))/(n) } =1.645* \sqrt{(0.1808(1-0.1808))/(2306) }=0.0132`

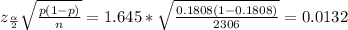
The boundaries are (p - e, p + e) = (0.1808 - 0.0132, 0.1808 + 0.0132) = (0.1676, 0.194)

The interval is (0.1676, 0.194)

d) We are 90% confident that the population proportion of adult Americans who have donated blood in the past two years is between 0.1676 and 0.194