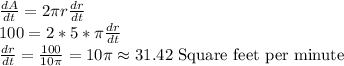Question

A rock is thrown into a still pond. The circular ripple move outward from the point of impact of the rock so that the area of the circle formed by a ripple increases at the rate of 100 square feet per minute. Find the rate at which the radius is changing at the instant the radius is 5 feet.

Answer 1

`\approx 31.42 \text{ Square feet per minute}`

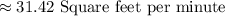
Explanation:

Area of the Pond A=
`\pi r^2`

The increase in the area of the pond as it moves outward is:
`(dA)/(dt)`

`(dA)/(dt)=(d)/(dt)\pi r^2\\(dA)/(dt)= 2\pi r (dr)/(dt)`

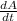
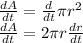
Since the area of the circle formed increases at the rate of 100 square feet per minute.

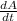`(dA)/(dt)` = 100 Square feet per minute

When the radius, r = 5 feet, we want to determine the rate at which the radius is changing,
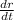`(dr)/(dt)`.

`(dA)/(dt)= 2\pi r (dr)/(dt)\\100=2*5*\pi (dr)/(dt)\\(dr)/(dt) =(100)/(10 \pi) =10 \pi \approx 31.42 \text{ Square feet per minute}`