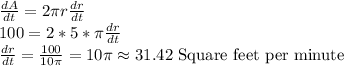Answer:
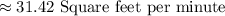
Explanation:
Area of the Pond A=
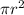
The increase in the area of the pond as it moves outward is:
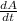
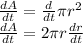
Since the area of the circle formed increases at the rate of 100 square feet per minute.
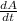 = 100 Square feet per minute
= 100 Square feet per minute
When the radius, r = 5 feet, we want to determine the rate at which the radius is changing,
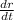 .
.