Question

Prove using mathematical induction that the number of permutations of the set {1, 2, . . . , n} with n elements is n!, for natural number n ≥ 1. As an example, the permutations of {1, 2, 3} are {[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]}.

Answer 1

Explanation:

We willl proof the statement using induction.

REcalll that to prove something using induction, we must prove it for a base case, then, we assume the result for n, and prove it for the case n+1.

Consider our base case as n=2, since n=1 is trival.

Note that given the set {1,2} the posible permutations are [1,2] and [2,1] (2 permutations). Recall that 2! = 1*2 = 2. So, the result applies to the base case.

Suppose that the result holds for n. That is, given a set {1,...,n} of n elements, the number of permutations is n!

Consider the case in which you have a set of n+1 elements {1,...,n,n+1}.

The total number of permutations of this set can be constructed as follows. Consider one permutation of the set {1, ...., n}. For illustration, consider the identity permutation. That is,

1, 2, 3, 4, ...., n. Recall that a permutation of the whole set can be constructed by taking one permutation of the set {1,...,n} and placing the element n+1. So, in our case, this are two examples of permutations of the new set :

n+1, 1,2,3,4,....,n.

1,n+1,2,3,4,...,n.

So, our problem reduces to count the total posibilities where we can place the last element n+1. Note, that we can place the last element in exactly n+1 positions to get n+1 permutations.

That means, that given one permutation of the set {1,...,n} we get n+1 permutations of the set {1,...,n+1}. Hence the total number of permutations of the set {1,...,n,n+1} is n+1 times the number of permutations of the set {1,...,n}. Using the induction hypothesis, we have that the number of permutations of the set {1,...,n,n+1} is

`n+1 \cdot n! = (n+1)!`

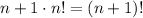
So, the result holds for any n.