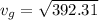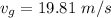Answer:
The tank is losing
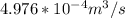
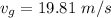
Step-by-step explanation:
According to the Bernoulli’s equation:
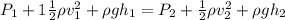
We are being informed that both the tank and the hole is being exposed to air :
∴ P₁ = P₂
Also as the tank is voluminous ; we take the initial volume
 ≅ 0 ;
≅ 0 ;
then
 can be determined as:
can be determined as:
![\sqrt{[2g (h_1- h_2)]](https://img.qammunity.org/2021/formulas/physics/high-school/vpdwhxplwtnlrf5m8nqrr9l8h24u34garx.png)
h₁ = 5 + 15 = 20 m;
h₂ = 15 m
![v_2 = \sqrt{[2*9.81*(20 - 15)]](https://img.qammunity.org/2021/formulas/physics/high-school/l5dlltjf2gr3j1hwrjthqepiccvzkrhxe4.png)
![v_2 = \sqrt{[2*9.81*(5)]](https://img.qammunity.org/2021/formulas/physics/high-school/jhvvsjd7xt72zufs516fn6fiuv28apyix2.png)
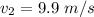 as it leaves the hole at the base.
as it leaves the hole at the base.
radius r = d/2 = 4/2 = 2.0 mm
(a) From the law of continuity; its equation can be expressed as:
J =
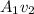
J = πr²

J =
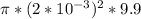
J =

b)
How fast is the water from the hole moving just as it reaches the ground?
In order to determine that; we use the relation of the velocity from the equation of motion which says:
v² = u² + 2gh ₂
v² = 9.9² + 2×9.81×15
v² = 392.31
The velocity of how fast the water from the hole is moving just as it reaches the ground is :