Question

A 620-g object traveling at 2.1 m/s collides head-on with a 320-g object traveling in the opposite direction at 3.8 m/s. If the collision is perfectly elastic, what is the change in the kinetic energy of the 620-g object? A 620-g object traveling at 2.1 m/s collides head-on with a 320-g object traveling in the opposite direction at 3.8 m/s. If the collision is perfectly elastic, what is the change in the kinetic energy of the 620-g object? It loses 0.23 J. It loses 1.4 J. It gains 0.69 J. It loses 0.47 J. It doesn't lose any kinetic energy because the collision is elastic.

Answer 1

It doesn't lose any kinetic energy because the collision is elastic.

Step-by-step explanation:

In an elastic collision, the momentum and kinetic energy are conserved

Answer 2

The answer is: It loses 0.23 J

Step-by-step explanation:

When the collision is elastic, both, momentum and kinetic energy is conserved, thus, the velocity is equal:

`v_(1) =((m_(1)-m_(2))/(m_(1)+m_(2) ) )u_(1)+(2m_(2)u_(2))/(m_(1)+m_(2))`

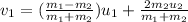
Where

m₁ = 620 g = 0.62 kg

m₂ = 320 g = 0.32 kg

u₁ = 2.1 m/s

u₂ = -3.8 m/s

Replacing:

`v_(1) =((0.62-0.32)/(0.62+0.32) )*2.1+(2*0.32*(-3.8))/(0.62+0.32) =-1.917m/s`

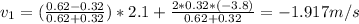
The change of kinetic energy is:

`E_(k) =(1)/(2) m*delta-v^(2) =(1)/(2) *0.62*((-1.917)^(2)-(2.1)^(2) )=-0.228=-0.23J`

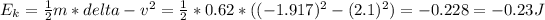
The negative sign indicates a loss of energy