Answer:
The answer is: It loses 0.23 J
Step-by-step explanation:
When the collision is elastic, both, momentum and kinetic energy is conserved, thus, the velocity is equal:
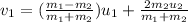
Where
m₁ = 620 g = 0.62 kg
m₂ = 320 g = 0.32 kg
u₁ = 2.1 m/s
u₂ = -3.8 m/s
Replacing:
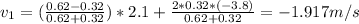
The change of kinetic energy is:
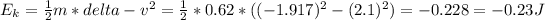
The negative sign indicates a loss of energy