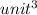Question

A right square pyramid with base edges of length $8\sqrt{2}$ units each and slant edges of length 10 units each is cut by a plane that is parallel to its base and 3 units above its base. What is the volume, in cubic units, of the new pyramid that is cut off by this plane?

Answer 1

32
`unit^(3)`

Explanation:

Given:

• The slant length 10 units
• A right square pyramid with base edges of length 8
  `√(2)`

Now we use Pythagoras to get the slant height in the middle of each triangle:

`\sqrt{10^{2 - (4√(2) ^(2) }) }` =
`√(100 - 32)` =
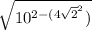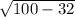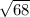`√(68)` units

One again, you can use Pythagoras again to get the perpendicular height of the entire pyramid.

`\sqrt{68-(4√(2) ^(2) )}` =
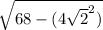`√(68 - 32)` = 6 units.

Because slant edges of length 10 units each is cut by a plane that is parallel to its base and 3 units above its base. So we have the other dementions of the small right square pyramid:

• The height 3 units
• A right square pyramid with base edges of length 4
  `√(2)`

So the volume of it is:

V = 1/3 *3* 4
`√(2)`

= 32
`unit^(3)`