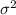Answer:
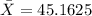
And the sample variance is given by:
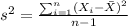
And replacing we got:
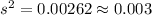
And this one is the best estimator for the population variance
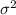
Explanation:
For this case we have the following data:
45.15,45.12,45.19,45.08,45.21,45.17,45.14,45.24
The first step would be calculate the sample mean given by:

And replacing we got:
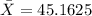
And the sample variance is given by:
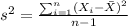
And replacing we got:
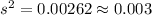
And this one is the best estimator for the population variance