Question

The following data show the number of hours per day 12 adults spent in front of screens watching​ television-related content. 1.8 4.7 4.1 5.2 7.6 7.3 5.7 3.2 5.4 1.9 2.7 8.1 a. Construct a 99 ​% confidence interval to estimate the average number of hours per day adults spend in front of screens watching​ television-related content.

Answer 1

99% Confidence interval: (2.9,6.7)

Explanation:

We are given the following data set:

1.8, 4.7, 4.1, 5.2, 7.6, 7.3, 5.7, 3.2, 5.4, 1.9, 2.7, 8.1

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

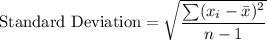
where
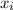`x_i` are data points,
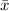`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`\bar{x} =\displaystyle(57.7)/(12) = 4.8`

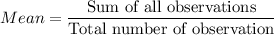
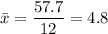
Sum of squares of differences = 51.18

`s = \sqrt{(51.18)/(11)} = 2.16`

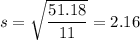
99% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

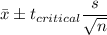
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 11 and}~\alpha_(0.01) = \pm 3.106`

`4.8 \pm 3.106((2.16)/(√(12)) )\\\\ = 4.8 \pm 1.937 \\\\= (2.863,6.737)\approx (2.9,6.7)`

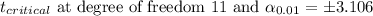
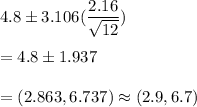
(2.9,6.7) is the required 99% confidence interval for average number of hours per day adults spend in front of screens watching​ television-related content.