Answer:
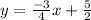
Explanation:
Our given points: (6, –2) and (–2, 4).
1. Use the slope formula to find the slope

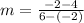
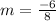
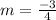
Therefore, the slope of the line is
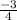 .
.
2. Substitute a point and a slope in point-slope form
Point-slope form:
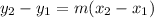
In point-slope form, the variables
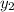 and
and
 stay y and x, so when we plug a point into this equation, we plug the x and y variables in
stay y and x, so when we plug a point into this equation, we plug the x and y variables in
 and
and
 . We can plug in either given point, (6, –2) and (–2, 4), for this equation to be correct. Below, you can see that I plugged in the first given point.
. We can plug in either given point, (6, –2) and (–2, 4), for this equation to be correct. Below, you can see that I plugged in the first given point.
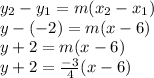
3. Distribute the slope through the parentheses
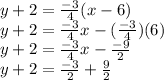
4. Solve for the y-variable
This is asking us to isolate the y variable in the equation that we have created in step 3. To isolate the y-variable, all we have to do is move the +2 over to the right side by subtracting both sides by 2.
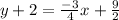
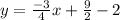
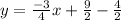
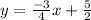
I hope this helps!