Answer:
The sample that would be required in order to estimate the fraction of people who black out at 6 or more Gs is of size 502.
Explanation:
The (1 - α)% confidence interval for population proportion p is:
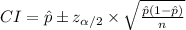
The formula to calculate the margin of error is,

The given information is,
 = 0.32 and margin of error = 0.03.
= 0.32 and margin of error = 0.03.
The z-value for 85% confidence level is,

*Use a z-table for the z-value.
Then the sample size n is given by,

![n=[(z_(\alpha/2)* √(\hat p(1-\hat p)))/(MOE) ]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/adfgqhxu3aij13ujcxaau55fe87fon9sv1.png)
![=[(1.44* √(0.32(1-0.32)))/(0.03)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/w5ex20niqedys3riwzrltbbhu9qlo1jnzu.png)
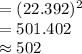
Thus, the sample that would be required in order to estimate the fraction of people who black out at 6 or more Gs is of size 502.