Answer:
The test statistic
Z = 1.149
Since the calculated value of Z = 1.149 is less than 1.96 at 5% (0.05) level of significance.
The null hypothesis is accepted
Hence the proportion is not equal 0.04
Explanation:
Given data a random sample of 300 circuits is tested, revealing 16 defectives.
The proportion of success

Null hypothesis:- H₀ = P ≠0.04
Alternative hypothesis:- H₁ = P =0.04
Q = 1-P = 1-0.04=0.96
Level of significance ∝ =0.05
The test statistic
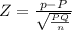
now substitute all values, we get
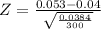
on calculation, Z = 1.149
Since the calculated value of Z = 1.149 is less than 1.96 at 5% (0.05) level of significance.
The null hypothesis is accepted .
Hence the proportion is not equal 0.04