Answer:
R=4.22*10⁴km
Step-by-step explanation:
The tangential speed
 of the geosynchronous satellite is given by:
of the geosynchronous satellite is given by:

Because
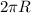 is the circumference length (the distance traveled) and T is the period (the interval of time).
is the circumference length (the distance traveled) and T is the period (the interval of time).
Now, we know that the centripetal force of an object undergoing uniform circular motion is given by:
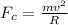
If we substitute the expression for
 in this formula, we get:
in this formula, we get:

Since the centripetal force is the gravitational force
 between the satellite and the Earth, we know that:
between the satellite and the Earth, we know that:
![F_g=(GMm)/(R^(2))\\\\\implies (GMm)/(R^(2))=(4m\pi ^(2)R)/(T^(2))\\\\R^(3)=(GMT^(2))/(4\pi^(2)) \\\\R=\sqrt[3]{(GMT^(2))/(4\pi^(2)) }](https://img.qammunity.org/2021/formulas/physics/high-school/no08w8yp2knef71dz78ce8h19op3t33p91.png)
Where G is the gravitational constant (
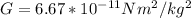 ) and M is the mass of the Earth (
) and M is the mass of the Earth (
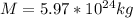 ). Since the period of the geosynchronous satellite is 24 hours (equivalent to 86400 seconds), we finally can compute the radius of the satellite:
). Since the period of the geosynchronous satellite is 24 hours (equivalent to 86400 seconds), we finally can compute the radius of the satellite:
![R=\sqrt[3]{((6.67*10^(-11)Nm^(2)/kg^(2))(5.97*10^(24)kg)(86400s)^(2))/(4\pi^(2))}\\\\R=4.22*10^(7)m=4.22*10^(4)km](https://img.qammunity.org/2021/formulas/physics/high-school/t9g1e56eyhfuknw48jdnxdo1l1uf5ohe3q.png)
This means that the radius of the orbit of a geosynchronous satellite that circles the earth is 4.22*10⁴km.