Question

There are 4 people at a party. Consider the random variable X=’number of people having the same birthday ’ (match only month, N=12). a. Define the sample space S and the associated probability function (pf). Plot pf. b. Plot the associated exceedance probability function G(x)=Pr[X>x]; c. Compute mean and standard deviation of X.

Answer 1

S = {0,2,3,4}

P(X=0) = 0.573 , P(X=2) = 0.401 , P(x=3) = 0.025, P(X=4) = 0.001

Mean = 0.879

Standard Deviation = 1.033

Explanation:

Let the number of people having same birth month be = x

The number of ways of distributing the birthdays of the 4 men = (12*12*12*12)

The number of ways of distributing their birthdays = 12⁴

The sample space, S = { 0,2,3,4} (since 1 person cannot share birthday with himself)

P(X = 0) =
`(12P4)/(12^(4) )`

P(X=0) = 0.573

P(X=2) = P(2 months are common) P(1 month is common, 1 month is not common)

P(X=2) =
`(3C2 * 12P2)/(12^(4) ) + (4C2 * 12P3)/(12^(4) )`

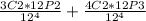
P(X=2) = 0.401

P(X=3) =
`(4C3 * 12P2)/(12^(4) )`

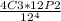
P(x=3) = 0.025

P(X=4) =
`(12)/(12^(4) )`

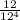
P(X=4) = 0.001

Mean,
`\mu = \sum xP(x)`

`\mu = (0*0.573) + (2*0.401) + (3*0.025) + (4*0.001)\\\mu = 0.879`

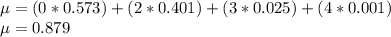
Standard deviation,
`SD = \sqrt{\sum x^(2) P(x) - \mu^(2)} \\SD =\sqrt{ [ (0^(2) * 0.573) + (2^(2) * 0.401) + (3^(2) * 0.025) + (4^(2) * 0.001)] - 0.879^(2)}`

SD = 1.033