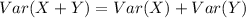Question

Let X and Y be discrete random variables. Let E[X] and var[X] be the expected value and variance, respectively, of a random variable X. (a) Show that E[X + Y ] = E[X] + E[Y ]. (b) If X and Y are independent, show that var[X + Y ] = var[X] + var[Y ].

Answer 1

(a)
`E[X+Y]=E[X]+E[Y]`

(b)
`Var(X+Y)=Var(X)+Var(Y)`

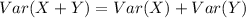
Explanation:

Let X and Y be discrete random variables and E(X) and Var(X) are the Expected Values and Variance of X respectively.

(a)We want to show that E[X + Y ] = E[X] + E[Y ].

When we have two random variables instead of one, we consider their joint distribution function.

For a function f(X,Y) of discrete variables X and Y, we can define

`E[f(X,Y)]=\sum_(x,y)f(x,y)\cdot P(X=x, Y=y).`

Since f(X,Y)=X+Y

`E[X+Y]=\sum_(x,y)(x+y)P(X=x,Y=y)\\=\sum_(x,y)xP(X=x,Y=y)+\sum_(x,y)yP(X=x,Y=y).`

Let us look at the first of these sums.

`\sum_(x,y)xP(X=x,Y=y)\\=\sum_(x)x\sum_(y)P(X=x,Y=y)\\\text{Taking Marginal distribution of x}\\=\sum_(x)xP(X=x)=E[X].`

Similarly,

`\sum_(x,y)yP(X=x,Y=y)\\=\sum_(y)y\sum_(x)P(X=x,Y=y)\\\text{Taking Marginal distribution of y}\\=\sum_(y)yP(Y=y)=E[Y].`

Combining these two gives the formula:

`\sum_(x,y)xP(X=x,Y=y)+\sum_(x,y)yP(X=x,Y=y) =E(X)+E(Y)`

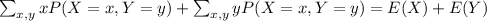
Therefore:

`E[X+Y]=E[X]+E[Y] \text{ as required.}`

(b)We want to show that if X and Y are independent random variables, then:

`Var(X+Y)=Var(X)+Var(Y)`

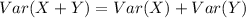
By definition of Variance, we have that:

`Var(X+Y)=E(X+Y-E[X+Y]^2)`

`=E[(X-\mu_X +Y- \mu_Y)^2]\\=E[(X-\mu_X)^2 +(Y- \mu_Y)^2+2(X-\mu_X)(Y- \mu_Y)]\\$Since we have shown that expectation is linear$\\=E(X-\mu_X)^2 +E(Y- \mu_Y)^2+2E(X-\mu_X)(Y- \mu_Y)]\\=E[(X-E(X)]^2 +E[Y- E(Y)]^2+2Cov (X,Y)`

Since X and Y are independent, Cov(X,Y)=0

`=Var(X)+Var(Y)`

Therefore as required:

`Var(X+Y)=Var(X)+Var(Y)`