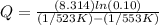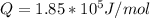Complete Question
Re crystallization is a thermally activated process. As such, can be characterized by the Arrhenius expression (Equation 1). As a first approximation we can treat
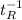 where
where
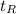 is the time necessary to fully recrystallize the micro structure. For a 50% cold-worked aluminum alloy, t_R is 100 hours at 250° C and 10 hours at 280°C .Calculate the activation energy for the Re crystallization process
is the time necessary to fully recrystallize the micro structure. For a 50% cold-worked aluminum alloy, t_R is 100 hours at 250° C and 10 hours at 280°C .Calculate the activation energy for the Re crystallization process
Equation 1
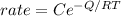
Answer:
The Activation energy is
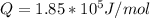
Step-by-step explanation:
From the question we are given the Arrhenius expression for the growth rate(Z) as
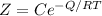
Where Q is the activation energy
C is known as the pre-exponential constant
R is the universal gas constant
T is the absolute temperature
From the question according to the first approximation the rate is inverse of time to fully recrystallize the micro structure(t_R)
We are told that at 250°C that
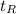 = 100 hours
= 100 hours
Now substituting into the Arrhenius expression
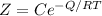
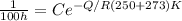
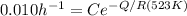 -----(2)
-----(2)
We are told that at 280°C that
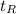 = 10 hours
= 10 hours
Now substituting into the Arrhenius expression
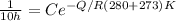
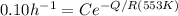 ----(3)
----(3)
Dividing the second equation by the first one
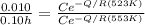
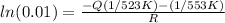
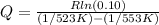
Substituting
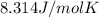 for R
for R