Answer:
(a) The volume flow rate is 5.43 × 10⁻³ m³/s
(b) The Reynolds's number is 251.1
The flow is laminar as the Reynolds's number is below the critical value of 2040
Step-by-step explanation:
Here, we have
The engine oil temperature = 60 °C
Plate gap = 3.60 m
Plate dimensions =
Length, L = 1.25 m
Width, W = 0.550 m
Inlet pressure = 1 atm
Viscosity of engine oil at SAE 10W - 60
μ = 31.946 mPa.s = 0.031946 kg/m·s
(a)
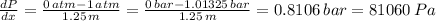
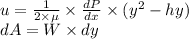
The rate of change of velocity is given by;
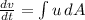

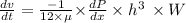
By substituting, we arrive at
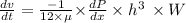
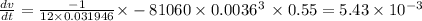
The volume flow rate is
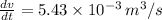
(b) The velocity, V is given by
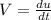
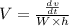 , we plug in the values and we have;
, we plug in the values and we have;
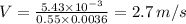
Reynolds's number is given by;
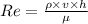
Where, ρ for the engine oil is 0.8130 g/cm³ = 813 kg/m³
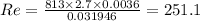
As the Reynolds's number value is less than 2040, the flow is laminar flow.