Question

cylinder shaped can needs to be constructed to hold 200 cubic centimeters of soup. The material for the sides of the can costs 0.02 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.07 cents per square centimeter. Find the dimensions for the can that will minimize production cost.

Answer 1

Radius=2.09 cm

Height,h=14.57 cm

Explanation:

We are given that

Volume of cylinderical shaped can=200 cubic cm.

Cost of sides of can=0.02 cents per square cm

Cost of top and bottom of the can =0.07 cents per square cm

Curved surface area of cylinder=
`2\pi rh`

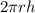
Area of circular base=Area of circular top=
`\pi r^2`

Total cost,C(r)=
`0.02* 2\pi rh+2\pi r^2* 0.07`

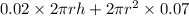
Volume of cylinder,
`V=\pi r^2 h`

`200=\pi r^2 h`

`h=(200)/(\pi r^2)`

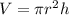
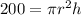
Substitute the value of h

`C(r)=0.02* 2\pi r* (200)/(\pi r^2)+2\pi r^2* 0.07`

`C(r)=(8)/(r)+0.14\pi r^2`

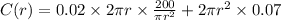
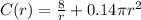
Differentiate w.r.t r

`C'(r)=-(8)/(r^2)+0.28\pi r`

`C'(r)=0`

`-(8)/(r^2)+0.28\pi r=0`

`0.28\pi r=(8)/(r^2)`

`r^3=(8)/(0.28\pi)=9.095`

`r=(9.095)^{(1)/(3)}=2.09`

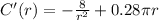
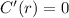
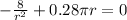
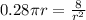
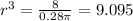
Again, differentiate w.r.t r

`C''(r)=(16)/(r^3)+0.28\pi`

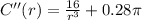
Substitute the value of r

`C''(2.09)=(16)/((2.09)^3)+0.28\pi=2.63>0`

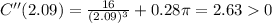
Therefore,the product cost is minimum at r=2.09

h=
`(200)/(\pi (2.09)^2)=14.57`

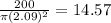
Radius of can,r=2.09 cm

Height of cone,h=14.57 cm