Answer:
0.2828.
Explanation:
From the information given:
- =98%=0.98
- P(Positive|No Cancer)=1.5%=0.015
- P(Cancer)=0.6%=0.006
Therefore: P(No Cancer)=1-P(Cancer)=1-0.006=0.994
We want to determine the probability that a person with a positive test result has cancer. i,e. P(Cancer|Positive)
Using Bayes Theorem for Conditional Probability
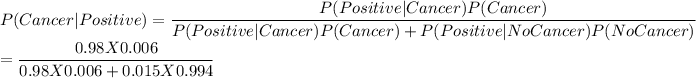
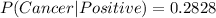
Therefore, the probability that a person with a positive test result has cancer is 0.2828.