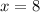Answer:
the equation of the axis of symmetry is
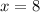
Explanation:
Recall that the equation of the axis of symmetry for a parabola with vertical branches like this one, is an equation of a vertical line that passes through the very vertex of the parabola and divides it into its two symmetric branches. Such vertical line would have therefore an expression of the form:
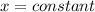 , being that constant the very x-coordinate of the vertex.
, being that constant the very x-coordinate of the vertex.
So we use for that the fact that the x position of the vertex of a parabola of the general form:
 , is given by:
, is given by:
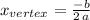
which in our case becomes:
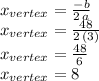
Then, the equation of the axis of symmetry for this parabola is: