Question

In △CDE , CD=14 , DE=9 , and m∠E=71∘ .

What is m∠D to the nearest tenth of a degree?

Enter your answer in the box.

m∠D = [ ]°

Answer 1

71.6°

Explanation:

CD/sinE = DE/sinC

14/sin(71) = 9/sinC

sinC = 0.60783337

C = 37.43300585

Angle D = 180 - 37.43300585 - 71

Angle D = 71.56699415

Answer 2

71.6 degrees

Explanation:

We can use the law of sines:
`(a)/(sinA) =(b)/(sinB)=(c)/(sinC)`

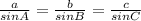
Here, we have:
`(14)/(sin71) =(9)/(sinC)`

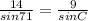
Solving for C, we have: 14 * sinC = 9 * sin71 ⇒ C = 37.4 degrees

To find angle D, we take 180 degrees and subtract angles E and C from it:

180 - 71 - 37.4 = 71.6 degrees.

Thus, the answer is 71.6 degrees.

Hope this helps!