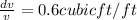Answer:
a)
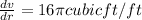
b) Approximate error of the volume increase when the radius changes from 2 to 2.4 ft = 0.6 that is
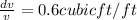
Explanation:
Explanation:-
a) Given Volume of spherical balloon
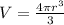 …(i)
…(i)
Differentiating with respective to the radius 'r'
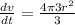
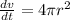
At r=2
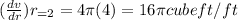
b) Step(1):-
Given Volume of spherical balloon
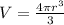

we property of logarithmic log(ab) = log a +log b
taking logarithmic on both sides , we get
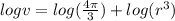 …(ii)
…(ii)
Step2:-
we will use
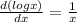
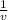 δ v = 0 +
δ v = 0 +
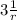 δ r
δ r
Given data radius changes from 2 to 2.4 ft
r+ δ r = 2.4 =2+0.4
here r =2 and δ r =0.4
Now
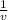 δ v =
δ v =

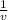 δ v = 0.6
δ v = 0.6
Approximate error in Volume = 0.6 cubic/ft
Approximate error of the volume increase when the radius changes from 2 to 2.4 ft = 0.6 that is