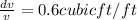Question

The volume Vequalsfour thirds pi r cubed of a spherical balloon changes with the radius. a. At what rate ​(ftcubed​/ft​) does the volume change with respect to the radius when r equals 2 ft question mark b. Using the rate from part a​, by approximately how much does the volume increase when the radius changes from 2 to 2.4 ft question mark

Answer 1

a)
`(dv)/(dr) = 16\pi cubic ft /ft`

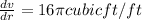
b) Approximate error of the volume increase when the radius changes from 2 to 2.4 ft = 0.6 that is

`(dv)/(v) =0.6 cubic ft /ft`

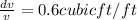
Explanation:

Explanation:-

a) Given Volume of spherical balloon

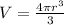`V = (4\pi r^(3) )/(3)` …(i)

Differentiating with respective to the radius 'r'

`(dv)/(dt) = (4\pi 3r^(2) )/(3)`

`(dv)/(dt) = 4 \pi r^(2)`

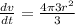
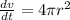
At r=2

`((dv)/(dr))r_(=2) =4\pi (4)=16\pi cubeft/ft`

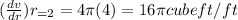
b) Step(1):-

Given Volume of spherical balloon

`V = (4\pi r^(3) )/(3)`

`logV = log((4\pi r^(3) )/(3))`

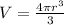
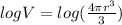
we property of logarithmic log(ab) = log a +log b

taking logarithmic on both sides , we get

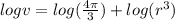`logv = log((4\pi )/(3) )+log(r^(3))` …(ii)

Step2:-

we will use
`(d(logx))/(dx) = (1)/(x)`

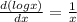
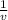`(1)/(v)` δ v = 0 +
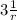`3 (1)/(r)` δ r

Given data radius changes from 2 to 2.4 ft

r+ δ r = 2.4 =2+0.4

here r =2 and δ r =0.4

Now
`(1)/(v)` δ v =
`3 X (1)/(2) X 0.4`

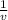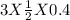
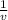`(1)/(v)` δ v = 0.6

Approximate error in Volume = 0.6 cubic/ft

Approximate error of the volume increase when the radius changes from 2 to 2.4 ft = 0.6 that is

`(dv)/(v) =0.6 cubic ft /ft`