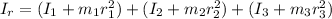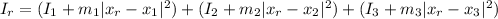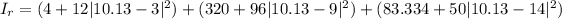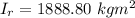Question

#198. Moment of inertia about center of a segmented bar A bar of width is formed of three uniform segments with lengths and areal densities given by: Matlab/Mathematica input: L1 = 6 rho1 = 1 L2 = 6 rho2 = 8 L3 = 4 rho3 = 5 What is the moment of inertia of the bar about the center of mass ?

Answer 1

Complete Complete

The complete question is shown on the first uploaded image

Answer:

The moment of inertia of the bar about the center of mass is

`I_r = 1888.80  \  kg m^2`

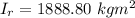
Step-by-step explanation:

The free body diagram is shown on the second uploaded image

From the diagram we see that is

The mass of each segment is

`m_1 = \rho_1  l_1 w = 1 * 6 * 2 = 12`

`m_1 = \rho_2  l_2 w = 8 * 6 * 2 = 96`

`m_1 = \rho_2  l_2 w = 5 * 5 * 2 = 50`

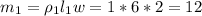
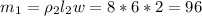
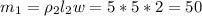
The distance from the origin to the center of the segments i.e the center of masses for the individual segments

`x_2 = (6)/(2) + 6 = 9 m`

`x_3 = (4)/(2) + 12 = 14 m`

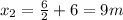
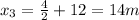
The resultant center of mass is mathematically evaluated as

`x_r = (m_1 * x_1 + m_2 *x_2 + m_3 *x_3)/(m_1 + m_2 + m_3)`

`=   (12 * 3 + 96 *9 + 50 *14)/(12+ 96 + 50)`

`x_r = 10.13m`

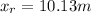
The moment of Inertia of each segment of the bar is mathematically evaluated

`I_1 =(m_1)/(12)(l_1^2 + w^2)` =
`(12)/(12)(1^2 + 2^2)`

`I_1 = 4 \ kgm^2`

`I_2 =(m_2)/(12)(l_2^2 + w^2)` =
`(96)/(12)(6^2 + 2^2)`

`I_2 = 320 \ kgm^2`

`I_3 =(m_3)/(12)(l_3^2 + w^2)` =
`(50)/(12)(4^2 + 2^2)`

`I_2 = 83.334 \ kgm^2`

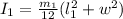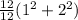
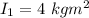
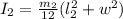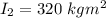
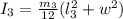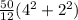
According to parallel axis theorem the moment of inertia about the center (
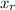`x_r`) is mathematically evaluated as

`I_r = (I_1 + m_1 r_1^2) + (I_2 + m_2 r_2^2) +(I_3 + m_3 r_3^2)`

`I_r = (I_1 + m_1 |x_r - x_1|^2) + (I_2 + m_2 |x_r - x_2|^2) +(I_3 + m_3 |x_r - x_3|^2)`

`I_r = (4  + 12 |10.13 - 3|^2) + (320 + 96 |10.13 - 9|^2) +(83.334 + 50 |10.13 - 14|^2)`

`I_r = 1888.80  \  kg m^2`