Answer:
a) 10.57% of the diameters are less than 25.0 mm
b) The 10th percentile of the diameters is 25.2024 mm
c) A diameter of 25.2 mm is on 89.44th percentile.
d) 88.81% of the diameter is between 25.0 and 25.3 millimeters
Explanation:
Given that:
mean μ = 25.1 mm
standard deviation σ = 0.08 mm
a) What proportion of the diameters are less than 25.0 mm?
The Z score is given by the equation:
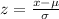
For diameter of 25mm
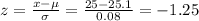
P(X < 25) = P(z < -1.25) = 0.1057 = 10.57%
10.57% of the diameters are less than 25.0 mm
b) Find the 10th percentile of the diameters
10th percentile = 0.1. From z table, the the 10th percentile corresponds with a z score of -1.28
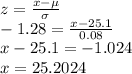
The 10th percentile of the diameters is 25.2024 mm
c) A particular ball bearing has a diameter of 25.2 mm. What percentile is its diameter on
The Z score is given by the equation:
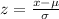
For diameter of 25.2 mm
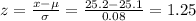
P(X < 25.2) = P(z < 1.25) = 0.8944 = 89.44%
A diameter of 25.2 mm is on 89.44th percentile.
d) To meet a certain specification, a ball bearing must have a diameter between 25.0 and 25.3 millimeters. What proportion of the ball bearings meet the specification
For diameter of 25 mm
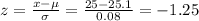
For diameter of 25.3 mm
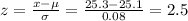
P(25 < X < 25.3) = P(-1.25 < z < 2.5) = P(z < 2.5) - P(z < -1.25) = 0.9938 - 0.1057 = 0.8881 = 88.81%
88.81% of the diameter is between 25.0 and 25.3 millimeters