Question

A process manufactures ball bearings with diameters that are normally distributed with mean 25.1 mm and standard deviation 0.08 mm. What proportion of the diameters are less than 25.0 mm? Find the 10th percentile of the diameters. A particular ball bearing has a diameter of 25.2 mm. What percentile is its diameter on? To meet a certain specification, a ball bearing must have a diameter between 25.0 and 25.3 millimeters. What proportion of the ball bearings meet the specification?

Answer 1

a) 10.57% of the diameters are less than 25.0 mm

b) The 10th percentile of the diameters is 25.2024 mm

c) A diameter of 25.2 mm is on 89.44th percentile.

d) 88.81% of the diameter is between 25.0 and 25.3 millimeters

Explanation:

Given that:

mean μ = 25.1 mm

standard deviation σ = 0.08 mm

a) What proportion of the diameters are less than 25.0 mm?

The Z score is given by the equation:

`z=(x-\mu)/(\sigma)`

For diameter of 25mm

`z=(x-\mu)/(\sigma)=(25-25.1)/(0.08) =-1.25`

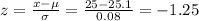
P(X < 25) = P(z < -1.25) = 0.1057 = 10.57%

10.57% of the diameters are less than 25.0 mm

b) Find the 10th percentile of the diameters

10th percentile = 0.1. From z table, the the 10th percentile corresponds with a z score of -1.28

`z=(x-\mu)/(\sigma)\\-1.28=(x-25.1)/(0.08)\\ x-25.1=-1.024\\x=25.2024`

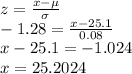
The 10th percentile of the diameters is 25.2024 mm

c) A particular ball bearing has a diameter of 25.2 mm. What percentile is its diameter on

The Z score is given by the equation:

`z=(x-\mu)/(\sigma)`

For diameter of 25.2 mm

`z=(x-\mu)/(\sigma)=(25.2-25.1)/(0.08) =1.25`

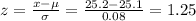
P(X < 25.2) = P(z < 1.25) = 0.8944 = 89.44%

A diameter of 25.2 mm is on 89.44th percentile.

d) To meet a certain specification, a ball bearing must have a diameter between 25.0 and 25.3 millimeters. What proportion of the ball bearings meet the specification

For diameter of 25 mm

`z=(x-\mu)/(\sigma)=(25-25.1)/(0.08) =-1.25`

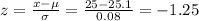
For diameter of 25.3 mm

`z=(x-\mu)/(\sigma)=(25.3-25.1)/(0.08) =2.5`

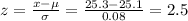
P(25 < X < 25.3) = P(-1.25 < z < 2.5) = P(z < 2.5) - P(z < -1.25) = 0.9938 - 0.1057 = 0.8881 = 88.81%

88.81% of the diameter is between 25.0 and 25.3 millimeters