Answer:
he sampling distribution of p is normal with mean p = 0.12
the standard deviation =
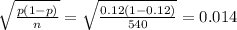
Explanation:
A sampling distribution is a probability distribution obtained from a larger number of samples gotten from a specific population. It shows all the possible result that can be gotten from each sample of a population
Given that:
p = 12% = 0.12
n = 540
the sampling distribution of p is normal with mean p = 0.12
the standard deviation =
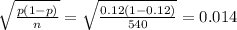
It is shown in the graph attached