Question

Ismael made a scaled copy of the following quadrilateral. He used a scale factor less than 111. What could be the length of the side that corresponds with AD, on the scaled copy of the quadrilateral?

a) 1/5 units.
b) 4 units.
c) 15.5 units.
d) 24 units.
e) 18 units.

Answer 1

A and B and C

Explanation:

i did it on khan

Answer 2

a) 1/5 units.

b) 4 units.

Explanation:

The picture of the question in the attached figure

we know that

If a the scale factor is less than 1 then the image is smaller than its original figure.

In this problem

The scale factor is less than 1

That means ----> The copy of the quadrilateral ABCD ls less than the original figure

To find out the length of the corresponding sides of the copy, multiply the length of the corresponding sides of the original figure by the scale factor.

Let

z ---> the scale factor

`A'D'=AD(z)`

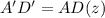
we have

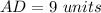`AD=9\ units` ---> see the picture

so

`A'D'=9z`

`z < 1`

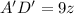
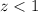
therefore

`A'D' < 9`

The length of the side that corresponds with AD, could be 1/5 units or 4 units