Question

A piece of copper wire is formed into a single circular loop of radius 13 cm. A magnetic field is oriented parallel to the normal to the loop, and it increases from 0 to 0.86 T in a time of 0.67 s. The wire has a resistance per unit length of 4.4 x 10-2 /m. What is the average electrical energy dissipated in the resistance of the wire? Number Units

Answer 1

0.07 J

Step-by-step explanation:

Parameters given:

Radius of loop, r = 13 cm = 0.13 m

Change in magnetic field, B = 0.86 T

Time taken, t = 0.67 s

Resistance per unit length of wire, R/L =
`4.4 * 10^(-2) ohms/m`

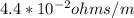
Resistance in the entire length of wire, R = R/L * L (where L = circumference of wire)

R =
`4.4 * 10^(-2) * 2\pi r = 4.4 * 10^(-2) * 2\pi * 0.13`

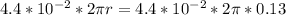
R = 0.036 ohms

Electrical energy is given as the product of Power and Time;

E = P * t

Electrical power, P, is given as:

`P = (V^2)/(R)`

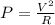
where V = EMF/Voltage

The average EMF induced in a coil is given as:

`V = (-BA)/(t)`

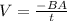
where A = Area of coil =
`\pi r^2` =
`0.13^2\pi = 0.0531 m^2`

Therefore, Power becomes:

`P = (((-BA)/(t))^2 )/(R)\\ \\\\P = ((BA)^2)/(Rt^2)`

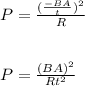
Then, Electrical energy becomes:

`E = ((BA)^2)/(Rt^2) * t\\\\\\E = ((BA)^2)/(Rt)`

`E = ((0.86 * 0.053)^2)/((4.4 *10^(-2) * 0.67))\\ \\\\E = 0.07 J`

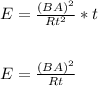
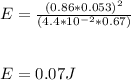
The average electrical energy dissipated in the resistance of the wire is 0.07 J