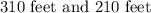Question

A farmer has 520 feet of fencing to construct a rectangular pen up against the straight side of a barn, using the barn for one side of the pen. The length of the barn is 310 feet. Determine the dimensions of the rectangle of maximum area that can be enclosed under these conditions. (Hint: Be mindful of the domain of the function you are maximizing.)

Answer 1

`310\text{ feet and }210\text{ feet}`

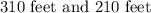
Explanation:

GIVEN: A farmer has
`520 \text{ feet}` of fencing to construct a rectangular pen up against the straight side of a barn, using the barn for one side of the pen. The length of the barn is
`310 \text{ feet}`.

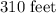TO FIND: Determine the dimensions of the rectangle of maximum area that can be enclosed under these conditions.

SOLUTION:

Let the length of rectangle be
`x` and
`y`

perimeter of rectangular pen
`=2(x+y)=520\text{ feet}`

`x+y=260`

`y=260-x`

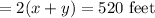
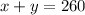
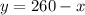
area of rectangular pen
`=\text{length}*\text{width}`

`=xy`

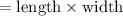
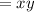
putting value of
`y`

`=x(260-x)`

`=260x-x^2`

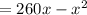
to maximize
`\frac{d \text{(area)}}{dx}=0`

`260-2x=0`

`x=130\text{ feet}`

`y=390\text{ feet}`

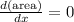
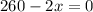
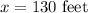
but the dimensions must be lesser or equal to than that of barn.

therefore maximum length rectangular pen
`=310\text{ feet}`

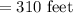
width of rectangular pen
`=210\text{ feet}`

Maximum area of rectangular pen
`=310*210=65100\text{ feet}^2`

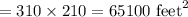
Hence maximum area of rectangular pen is
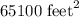`65100\text{ feet}^2` and dimensions are
`310\text{ feet and }210\text{ feet}`