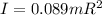Question

What is the rotational inertia of an object that rolls without slipping down a 2.00-m-high incline starting from rest, and has a final speed of 6.00 m/s at the bottom? Express the rotational inertia as a multiple of mr^2, where is the mass of the object and is its radius

Answer 1

We will apply the concepts of energy conservation to solve the problem. We know that gravitational potential energy is equivalent to the sum of translational kinetic energy and rotational kinetic energy. Additionally, the relation of the angular velocity with the tangential velocity will be determined to eliminate the angular term and obtain the expression of the Inertia in terms of the data given, therefore, we know that

`PE_(g) = KE_(trans) +KE_(rot)`

`mgh = (1)/(2) mv^2+(1)/(2)I\omega^2`

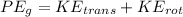
The angular velocity in terms of tangential velocity and radius is defined as,

`\omega = (v)/(R)`

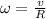
Replacing,

`mgh = (1)/(2) mv^2+(1)/(2) I((v)/(R))^2`

Multiplying by R^2,

`gh(mR^2) = (v^2)/(2) (mR^2)+(v^2)/(2)I`

`(v^2)/(2)I = (gh-(v^2)/(2))mR^2`

`I = ((2gh)/(v^2)-1)mR^2`

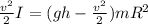
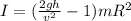
Replacing with our values we have,

`I = ((2(9.8)(2))/(6^2)-1)mR^2`

`I = 0.089mR^2`